


Trading Crypto With Leverage
Trading cryptocurrencies like bitcoin or ether with leverage has become increasingly popular. Many crypto exchanges offer 10x or even 100x leverage on BTC or ETH. However, the volatility of these assets may surprise beginners. This article helps beginners build intuition for leverage trading and empowers them to manage the risk in these positions more effectively by rethinking their position sizes in light of their collateral balances.
Imagine you know that the expected return of ether over the next year will be +30%. By ‘know the expected return’ we mean that the return is random, but you know that on average it will be +30%. You have $1000 to trade with. Naturally you might want to use a bunch of leverage to maximize your gain from your knowledge. You also know ETH is a volatile asset and you don’t want to be liquidated before your knowledge about the expected return can play out. Let’s try and develop some intuition for how much leverage might be reasonable to use.
This is an exceptional scenario! You have real alpha in the sense that you know the expected return of ETH over the next year. Let’s imagine that you decide to try a 5x levered long. This choice seems relatively restrained. After all, dYdX offers even greater leverage! And you have actual alpha!
Simulating Leverage Trading
Let’s simulate the results of the choice to go 5x long ETH 10,000 times and see what happens. Before looking further, what do you think the chance you get liquidated and lose everything is?
The animation below illustrates the first ~thousand return paths for ETH that we simulated.
By the end of the simulation ~70% of the return paths have resulted in liquidation. Indeed, many of the paths that eventually end up 50% or more in the money are liquidated before they get there. The return paths average +30% but most traders would never get the benefit of that return if they choose 5x leverage. This result can be generalized across more of the parameter space by exploring more possible expected return values and leverage choices.
How Risky is Leverage
As noted above, in our initial experiment with 30% expected return and 5x leverage we have a 70% chance of liquidation by the end of the year. The table below shows liquidation probabilities across different levels of leverage and expected return (alpha).
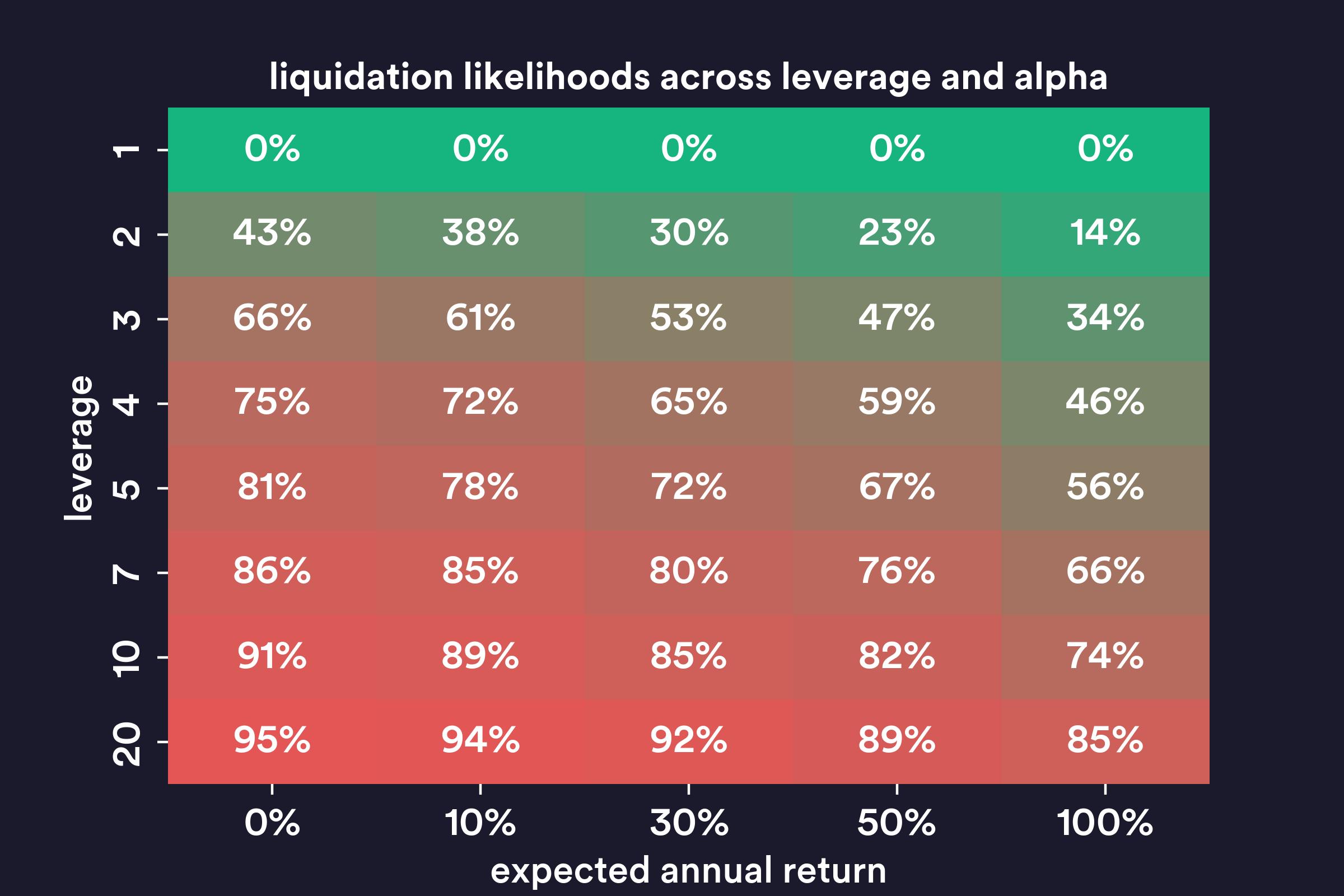
Intuitively, the more alpha you have, the lower chance of liquidation and the more leverage you have, the higher chance of liquidation. Even if you have truly huge alpha (expected return 100%) using 5x leverage results in more than a 50% chance to get liquidated by the end of the year.
Implications for Portfolio Management
Notably, a higher chance of liquidation isn’t necessarily indicative of a lower expected return. In fact, in the simulations referenced above, on average you still make more money with more leverage under some conditions.
The tradeoff is more about risk management, which is illustrated by a simple example: Would you rather have a 1 in 20 chance to make $40 or a 1 in 2 chance to make $2? The expected return of the former is higher, but so is its uncertainty. If you can aggregate a large number of independent positions that look like the former (i.e., high expected value, high variance), then you can reduce the variance and end up with a great portfolio. If you can only enter into one position you may want to pick the latter. Setting stop-loss orders will help avoid liquidation, but will not improve your ability to weather drawdowns and continue to hold a position long enough to realize your alpha.
Leverage is certainly not always bad. In a future piece we will discuss how leverage allows for hedged portfolios to be levered up to allow for capital-efficient positions in specific risks.
Technical Aside on the Choice to Simulate Return Streams
It’s not necessary to understand this section fully to appreciate the conclusions of the article so far, but it’s included for completeness.
We chose to simulate the return of ether as drawing from a lognormal distribution. The mean of this distribution was set by our expected return and the dispersion was set to a value derived empirically.
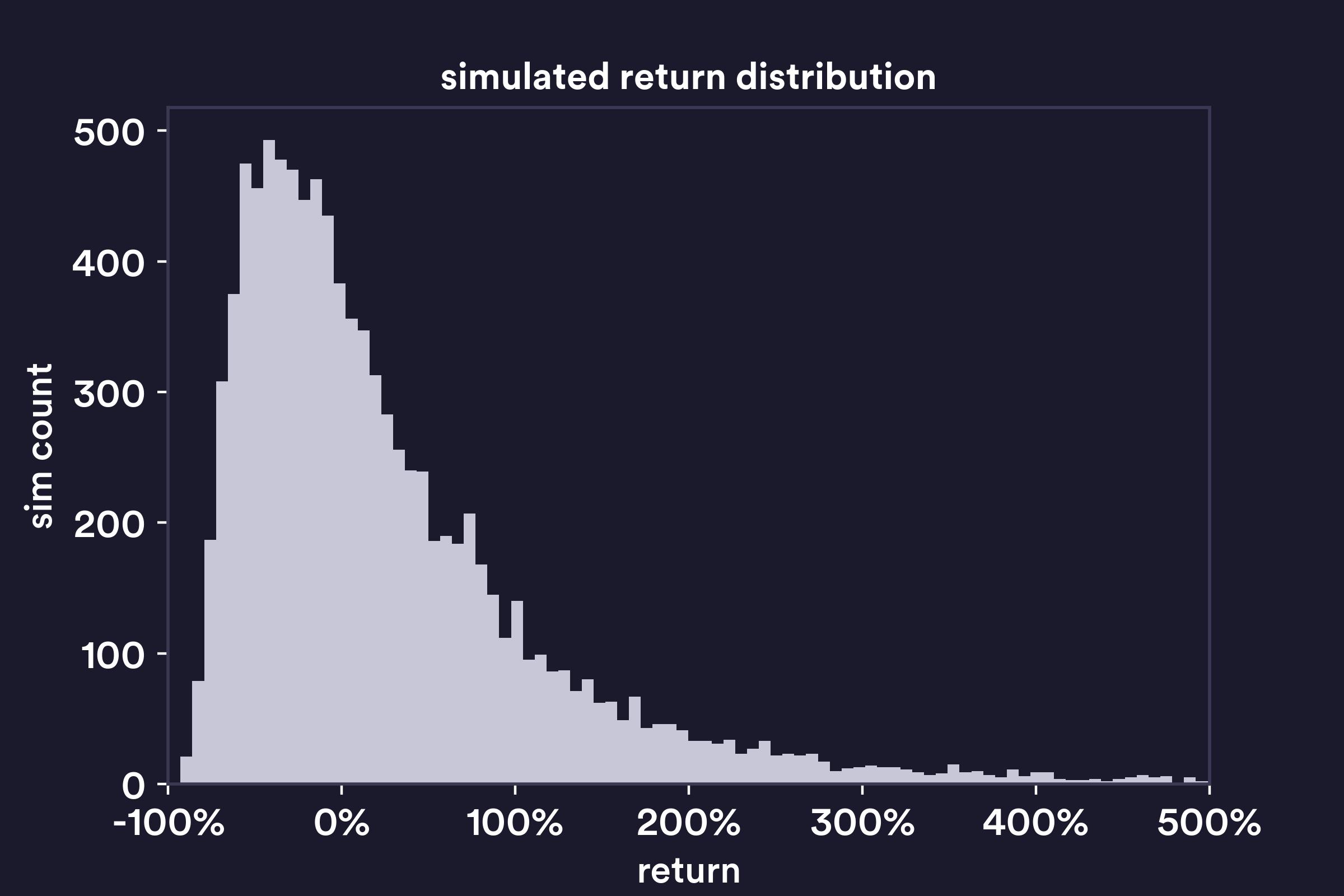
When writing this article, we initially intended to set up an integral to solve for the probability of getting liquidated. In a somewhat similar setup (normal returns, no drift) we found a helpful discussion in Introduction to Probability Models on page 611. However, for the setup in this piece (lognormal, non-zero drift) we couldn’t find any method that seemed easier than just simulating a large number of trials. Below we show a histogram of the cumulative simple returns for the simulation with an expected simple return of +30%.
The notebook that did the simulations and created the charts in this article is available in this repo.
The opinions and information presented in this article (the “Article”) are provided for general information purposes only, and are strictly those of the persons or individuals expressing such opinions and information (the “author(s)”), and are not representative of any other person, including dYdX Trading Inc. or any affiliate, agent, or representative thereof (“dYdX”). Reference to any specific product or entity does not constitute an endorsement or recommendation by dYdX. The content provided in this Article does not constitute, and should not be considered, or relied upon as, financial advice, legal advice, tax advice, investment advice, or advice of any other nature. The information in this Article is not a call to action to purchase any investment, or crypto-asset, of any kind (the “Service”). By using the Service, you agree that you are responsible to conduct independent research, perform due diligence, and engage a professional advisor prior to taking any financial, tax, legal or investment action related to the subject matter presented. Neither this Article, nor the author offers the purchase or sale of securities. By using the Service, you agree that neither dYdX nor the author is responsible, directly or indirectly, for any damage or loss incurred by you in connection with the use of or reliance on any content, goods or services mentioned in this published media.